木上の等高線集約クエリ

(追記 2022/03/27 23:07)

変種 1, 1' に対する可逆性を仮定しない解法を教えて頂きました．詳細は以下の記事を参照してください．

noshi91.hatenablog.com

www.mathenachia.blog

(追記終)

次のような問題を考えます．

問題

$N$ 頂点の木 $T$ が与えられる．$v\in\{1,\ldots, N\}$ に対して，頂点 $v$ の重みは $W _ v$ で初期化されている．以下の形式で表されるクエリが $Q$ 個与えられるので，順番に処理せよ．

1 v x : 頂点 $v$ の重みを $x$ に更新する．即ち，$W _ v \leftarrow x$ とする．
2 v d : 頂点 $v$ からの最短距離が $d$ であるような頂点の集合を $S(v,d)$ として，$\displaystyle \sum _ {u \in S(v,d)} W _ u$ を出力する．

ここで，頂点 $u$ と頂点 $v$ の最短距離を木 $T$ 上の $u, v$ パスの辺数の最小値と定義します．

観察

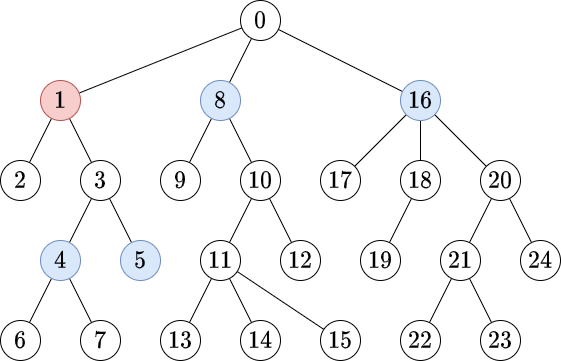
例として以下の図のような木を考えます．また，頂点の重み $W _ i$ は，理解の簡単のため $W _ i = i$ としておきます．

集約クエリを容易に計算できる例として，根に対するクエリが考えられます．以下の図は，頂点 $v=0$ から距離 $d=2$ の頂点を集約するクエリを表しています．赤の頂点が $v$ (以降，これを原点と呼びます)，青の頂点は原点 $0$ から距離 $2$ の集約対象の頂点を表しています．このとき，出力すべき値は $W _ 2 + W _ 3 + W _ 9 + W _ {10} + W _ {17} + W _ {18} + W _ {20} = 2+3+9+10+17+18+20=79$ となります．

この場合は，幅優先探索の訪問順に頂点番号を振り直すことで区間和を求めるクエリに帰着されます．従って，原点として根しか選ばれない場合は，頂点の重みの和を Segment Tree などを用いて管理することで，タイプ 1 , 2 のクエリを各 $O(\log N)$ time で処理することが出来ます．

難しいのは，原点として根以外が選択される場合です．以下の図は，原点 $1$ から距離 $2$ の頂点を集約するクエリを表しています．このとき，出力すべき値は $W _ 4 + W _ 5 + W _ 8 + W _ {16} = 4 + 5 + 8 + 16 = 33$ となります．

この場合，先述の方法で頂点番号を振り直したとしても，最悪の場合は $\Theta(\sqrt{N})$ 個の区間に分割されます $(\star 1)$．最悪ケースの一例としては，以下のようなケースが考えられます．

$(\star 1)$ の補足

原点 $v$ から距離 $d$ の頂点を集約するクエリを考えます．

$v$ から $k\; (0\leq k \leq d)$ 回親を辿ったあと，$v$ が属さない部分木に $d - k$ 回潜ることで到達できる頂点は集約対象の頂点であり，その深さは $\mathrm{de p}(v) + d - 2 k$ と表されます．逆に，全ての集約対象の頂点はこれで尽くされます．

親方向に辿る頂点は異なる $k$ で共有できますが，部分木に潜る際に辿る頂点は異なる $k$ で共有できません．従って，集約対象の頂点たちが $l$ 種類の深さを持つとすれば，頂点は少なくとも $0 + 1 + \cdots + (l - 1) = l (l - 1) / 2$ 個必要であり，集約対象となる頂点の深さの種類数は $O(\sqrt{N})$ であることが示されます．各深さに対して区間は高々 2 つなので，上界を $O(\sqrt{N})$ で抑えられることが示されます．

下界に関しては，図の構築を一般化することで示されます．(補足終)

本記事では，上記の方法 ¹ よりも高速にクエリを処理することを目指します．

解法

前計算

唐突ですが，重心分解を用いて本問題を解くことを考えます．重心分解の過程を表す木 $G _ T$ を作ります．$G _ T$ は，次の手続きによって生成される根付き木です．

$T$ の重心の 1 つを任意に選んで $c$ とする．
- $T$ がただ 1 つの頂点からなる場合は，頂点 $c$ のみからなる，$c$ を根とする根付き木を返す．
- $T$ が 2 つ以上の頂点からなる場合は，$T$ から頂点 $c$ と $c$ に接続する全ての辺を削除して出来る森の各連結成分ごとに再帰的に本手続きを行う．その結果返された根付き木 $X _ 1, \ldots, X _ k$ を頂点 $c$ の子する，$c$ を根とする根付き木を返す．

「観察」の節で例示した木 $T$ に対しては，例えば以下のように $G _ T$ は構築されます (重心が 2 つある場合の選択には任意性があるため，必ずしも図の通りになるとは限りません)．

追記 (2023/11/22) 次の図以降、誤って頂点 $5$ と $7$ を逆に描いてしまっています。また、頂点 $12$ と $15$ も逆に描いてしまっています。画像データを紛失したので、ここで注記するだけに留めさせてください。すみません。 (追記終)

上記の手続きにおいて，$T$ のすべての頂点はちょうど $1$ 回ずつ重心として選択されます．即ち，$G _ T$ の頂点集合 $V(G _ T)$ と $V(T)$ は一致します．ここで，頂点 $v$ が重心として選択された時点の $v$ を含む連結成分は木となります．これを $v$ を根とする根付き木とし，$U _ v$ で表します．

各 $v$ に対して，$V(U _ v)$ を $U _ v$ における幅優先探索の訪問順に並べ替え，頂点の重みの和を管理する Segment Tree $\mathrm{Seg} _ v$ を構築しておきます．「観察」の節で述べたように，この前計算により $U _ v$ に対する原点を $v$ とする集約クエリおよび重みの更新クエリを効率的に処理することが出来ます．

さて，$G _ T$ の高さは $O(\log N)$ と評価されること $(\star 2)$，および $\displaystyle \sum _ { v = 0 } ^ { N - 1} | V(U _ v) | = O(N \log N)$ が成立すること $(\star 3)$ などから，ここまでの前計算は全体 $O(N \log N)$ time で可能です．

$(\star 2)$ の補足

$G _ T$ における $v$ の親を $p$ とすれば，重心の定義から $|V(U _ v)| \leq \dfrac{1}{2} |V(U _ p)|$ が成立します．$G _ T$ の根 $r$ について $|V(U _ r)| = N$ であること，および任意の頂点 $v$ に対して $|V(U _ v)| \geq 1$ であることから，$G _ T$ の高さが $O(\log N)$ であることが従います．(補足終)

$(\star 3)$ の補足

$G _ T$ において深さが等しい任意の相異なる頂点 $u, v$ に対して $V(U _ u) \cap V(U _ v) = \empty$ が成り立ちます．従って，$G _ T$ において深さが $d$ であるような頂点の集合を $S _ d$ とすれば，任意の $d$ に対して $\sum _ { v \in S _ d } | V(U _ v) | \leq N$ が成り立ちます．$G _ T$ の深さの最大値は $O(\log N)$ であったので，$\sum _ {v = 0} ^ {N - 1} | V(U _ v) | = O(N \log N)$ と評価されます．(補足終)

クエリ処理

更新クエリ

頂点 $v$ に対する更新クエリを考えます．全ての Segment Tree に正しい情報を持たせておくためには，$v \in V(U _ w)$ を満たす全ての頂点 $w$ に対して $\mathrm{Seg} _ w$ を更新する必要があります．$G _ T$ の定義から，$v \in V(U _ w)$ であるための必要十分条件は $G _ T$ において $v$ から親を $0$ 回以上辿ることで $w$ に到達可能であることです．$G _ T$ の高さは $O(\log N)$ であったので，そのような $w$ は $O(\log N)$ 個しかありません．$\mathrm{Seg} _ w$ の更新は $O(\log N)$ time で可能なので，全体 $O( (\log N) ^ 2)$ time で更新クエリを処理することが出来ました．なお，$\mathrm{Seg} _ w$ において頂点 $v$ の値が格納されている添字を高速に取得できる必要がありますが，これは前計算の計算量を悪化させることなく可能です．

集約クエリ

頂点 $v$ から距離 $d$ の頂点の重みの総和 $\displaystyle \sum _ {u \in S(v, d)} W _ u$ を求めるクエリを考えます．

まず，「観察」の節で述べたように，$\displaystyle \sum _ {u \in S(v, d) \cap V(U _ v)} W _ u$ は $\mathrm{Seg} _ v$ に対する区間和取得クエリとなり容易に計算されるので，答えに足し込んでおきます．

続いて，$G _ T$ における $v$ の親 $p$ に対して，$\displaystyle \sum _ {u \in (S(v, d) - V(U _ v)) \cap V(U _ p)} W _ u$ を計算することを考えます．このとき，$U _ p$ における $p$ の子であって，$v$ と一致するか，あるいは $v$ を子孫に持つような頂点が存在するのでこれを $c$ とします．$c$ を根とする子部分木の根を $v$ に変更すれば，$U _ v$ と一致します．即ち，$c$ を根とする子部分木に含まれる頂点であって，$v$ からの距離が $d$ であるような頂点の重みの和は既に答えに足し込まれています．

従って，下図のように，$\displaystyle \sum _ {u \in (S(v, d) - V(U _ v)) \cap V(U _ p)} W _ u$ は $\mathrm{Seg} _ p$ における高々 2 つの区間の和として計算することが出来ます．

適切な前計算により $c$ や $\mathrm{Seg} _ p$ で和を取るべき区間，$p$ と $v$ の距離 $\mathrm{dist}(v, p)$ は $O(1)$ time で求めることができます $(\star 4)$．従って，$\displaystyle \sum _ {u \in (S(v, d) - V(U _ v)) \cap V(U _ p)} W _ u$ も $O(\log N)$ time で計算することが出来ました．

$(\star 4)$ の補足

例えば，LA や LCA を前計算 $O(N)$ time，クエリ $O(1)$ time で求めるアルゴリズムが存在するので，それらを用いることで前計算の計算量を悪化させること無く達成されます．

あるいは，集約クエリの計算中に現れる $p,v$ の組は $O(N \log N)$ 通りであることを用いて全て前計算することによっても達成可能です．後者の方法は特別なライブラリを必要としないこと，クエリが配列へのアクセスだけで済むことが利点ですが，前計算がやや重くなることが欠点です．

さらに別の選択肢として，$O(\log N)$ time を許容して HLD などで対応しても Segment Tree で区間和を計算するのに結局 $O(\log N)$ time だけ掛かるため集約クエリの計算量は悪化しません．好みに合わせて実装してください．(補足終)

同様の計算を $G _ T$ の根まで遡りながら行うことで，クエリの答えを計算することが出来ます．$G _ T$ の高さは $O(\log N)$ であったので，全体 $O( (\log N) ^ 2)$ time で集約クエリを処理することが出来ました．

実装

私のライブラリへのリンクを張っておきます．

https://suisen-cp.github.io/cp-library-cpp/library/tree/contour_aggregation_query_on_tree.hppsuisen-cp.github.io

問題例

C - 木の問題

全ての頂点の重みを $1$ として集約クエリを投げるだけです．

おまけ

問題の変種を考えます．

変種 1

タイプ 2 のクエリを次のように変更することが考えられます．

2 v d : 頂点 $v$ からの最短距離が $d$ 以下であるような頂点の集合を $S(v,d)$ として，$\displaystyle \sum _ {u \in S(v,d)} W _ u$ を出力する．

元の問題と同様の方法で解こうとすると，下図のように，集約クエリにおいて $\mathrm{Seg} _ p$ で和を取る必要のある区間 (青で囲った部分) の個数が定数個ではなくなってしまいます．

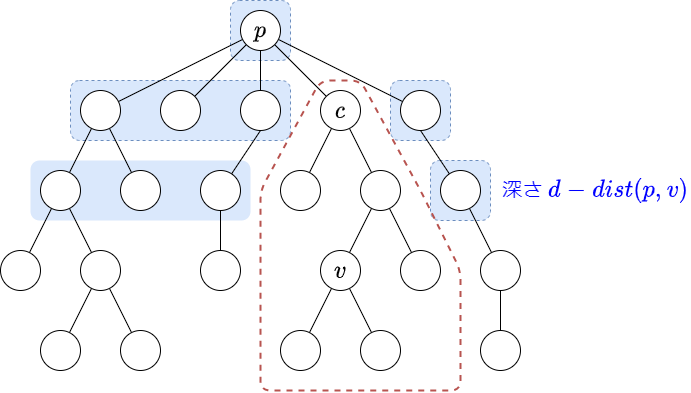
そこで，下図のように，一旦必要の無い部分を含めた総和 (青で囲った部分) を求めた後に不要な部分 (赤で囲った部分) を差し引くことを考えます．

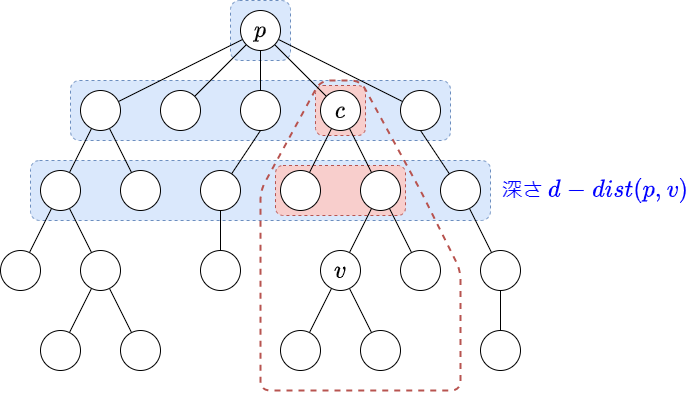
$p$ の全ての子 $c$ に対して，$U _ p$ における $c$ を根とする子部分木の頂点を BFS の訪問順に並べ替えて Segment Tree $\mathrm{Seg} _ {p, c}$を構築しておくことで，差し引くべき値は $\mathrm{Seg} _ {p, c}$ におけるある区間和として表現され，元の問題と同じ計算量オーダーで問題を解くことが出来ます．

ただし，元の問題は集約クエリの二項演算が可換モノイドであることのみを要求していましたが，この変種においては加えて可逆性が必要であり，即ち可換群であることを要求します ²．

変種 1'

変種 1 の自然な拡張です．タイプ 2 のクエリを次のように変更します．

2 v l r : 頂点 $v$ からの最短距離が $l$ 以上 $r$ 以下であるような頂点の集合を $S(v,l,r)$ として，$\displaystyle \sum _ {u \in S(v,l,r)} W _ u$ を出力する．

可逆性を仮定すれば，($l$ 以上 $r$ 以下の総和) = ($r$ 以下の総和) - ($l - 1$ 以下の総和) として解けます．

変種 2

タイプ 3 のクエリを追加します．Segment Tree -> Lazy Segment Tree みたいな気分です．

3 v d f : 頂点 $v$ からの最短距離が $d$ であるような頂点の集合を $S(v,d)$ として，全ての $u \in S(v,d)$ に対して $W _ u \leftarrow f \cdot W _ u$ とする．

これは，現在の方法では，全ての $\mathrm{Seg} _ v$ に正しい情報が乗った状態を効率的に保つのが難しいです．高速に解けたら教えてください．

この方法でも $O(\sqrt{N})$ 個の区間にはなるので愚直よりは良い計算量オーダーが得られているように思われますが，その $O(\sqrt{N})$ 個の区間を高速に求められるかはまた別の問題で，これは結構難しそうだと思っています．↩
可逆性を要求せずに計算量オーダを悪化させずに解く方法は思いつきませんでした．出来たら教えてください．↩